QUANTUM LOGIC WITH IMPLICATION
J . JAY ZEMAN
The non-classical nature of quantum theory has led to a number of efforts to formalize the logic of statements whose universe of discourse is the subatomic (see, for example, [3], [6], [8], and [10]). It might be hoped that ideally the fruit of such efforts would be a formalism not totally divorced from the classical logic, but incorporating or incorporated in it in such a manner as to unify the logic of the micro- and the macro-worlds. Indeed, this has been the general direction taken by these efforts, including that which we principally examine and expand upon here.* Josef Jauch, [6], pp. 67-89, developed a "propositional calculus of quantum mechanics". He objected to calling a system like his a "logic of quantum mechanics"; however, our use of 'logic' here is not, I think, the use to which Jauch objected. A logic, for our present purposes, is a mathematical formalism having a reasonable interpretation as a theory of deduction; its actual application as normative of argumentation in reality is a matter of empirical judgment. This seems close to the way Jauch wished to use "propositional calculus" but more general, allowing for extension to a quantification theory of quantum mechanics, for example.
Although Jauch's presentation of a propositional calculus of quantum mechanics is mathematically interesting and suggestive, there are a number of. problems connected with it. It is our purpose to engage some of these problems and to present a rigorously defined formalism intended to come close to doing the job intended by Jauch for his logic. The success or lack of success of this effort as related to actual application of this formalism in the foundations of quantum theory is, I think, a matter for the physicists to decide; the empirical judgment involved in this application is not in the scope of this paper.
If a formalism is to have a reasonable interpretation as a theory of
deduction, it seems clear that it must include a relation which, when it holds
between two elements of the formalism, may be reasonably interpreted as
expressing that one of the elements 'follows from' the other, in some sense of
'follows from'. Such a relation may be termed, in general, an implication
relation. To be a logic, then, a formalism must possess an implication relation.
Jauch recognized this, but unfortunately identified what he calls 'implication'
with the partial-ordering relation in the lattice-theoretical presentation of
his logic. This will not do, for implication is a propositional connective and
so is the same kind of linguistic object as are other propositional connectives,
such as conjunction, disjunction, negation. These last-named connectives
correspond respectively to the meet, join, and complementation of a
lattice-theoretical presentation, and so the object in the lattice-theoretical
presentation corresponding to implication should be the same sort of object as
are meet and join, that is, it should form elements from elements of the
lattice. The partial-ordering relation, however, forms statements from elements
of the lattice, and so is a different breed of cat, corresponding to the
metatheoretical deduction relation (commonly expressed by the turnstile: ![]() )
. The identification of implication with partial-ordering, then, amounts to a
violation of the metalanguage/object-language distinction.
)
. The identification of implication with partial-ordering, then, amounts to a
violation of the metalanguage/object-language distinction.
It may be objected that we are splitting hairs here, since the deduction relation and implication are commonly thought of as being rather intimately associated; indeed, if implication is considered as it is most commonly understood, the statement
| (1) | a, G |
(where G is any set of statements) holds. It might seem, then, that all that is needed to correct this problem is to introduce a new operator into Jauch's lattice; call it the implication operator 'É', and let a É b be an element when a and b are. As an additional axiom to the lattice-theoretical presentation we would then add the correlate of (1):
| (2) | c Ù a £ b iff c £ a É b |
Simple as this seems, it will not do for this case. The result of adding (2) to a lattice is an implicative lattice and, as noted in [4], p. 144, for example, every implicative lattice is distributive. Distributivity is one of the properties which it is generally agreed a quantum logic should lack, and so (2) cannot be part of a lattice which is to be employed as a quantum logic.
Now (1) or (2) is sufficient as a postulate for pure positive implication, which means that even intuitionistic (and a fortiori classical) implication is too strong for a quantum logic. A number of pure implicational calculi weaker than or independent from positive implication are available (see, for example, [2], [5], and [11]); is it possible that one of them can provide a basis for quantum implication? We find a clue in Jauch's brief semantical discussion of quantum conjunction in terms of "filters" constructed from "yes-no experiments" (experiments which assign a truth-value--true or false--to a given statement) [6], pp. 72-5. He noted that in quantum, as opposed to classical, physical systems, it may make sense to ask about either of a pair of statements p and q considered separately, but no sense to ask about the truth or falsity of the statement which is the conjunction of p and q, since the measurement used to determine the truth-value of p may so modify conditions as to affect the subsequent measurement of the truth-value of q. Jauch proposed that the difficulty be handled by using not just one pair of yes-no experiments (one for p and one for q) as a "filter" for the conjunction of p and q, but an infinite sequence of yes-no experiments, alternating for p and q as a filter for Kpq. Kpq would then be judged true iff both p and q "passed" the compound filter, that is, received true as their values in all the component yes-no experiments.
This idea is immediately suggestive of Kripke-style semantics for modal logic [7]. Each pair of yes-no experiments for p and q can be considered located in a 'possible world' (an element of a Kripke model-structure), with the accessibility relation between these possible worlds being determined by the order of the experiments in the sequence; if one p/q pair of experiments occurs before another, then the 'world' of the first has access to that of the second. Kpq is then true on Jauch's interpretation in a given world iff p and q are true in every world to which that one has access, i.e., in every succeeding pair of yes-no experiments. From this point of view, it is clear that Jauch's condition for the truth of Kpq is actually too strong; it has the effect of making quantum conjunction into necessary conjunction. Jauch's logic is a lattice, and so every element will be identical to its meet with itself, and so CpKpp must hold. But it cannot, given the "filter" suggested for K, for suppose p and q are to be tested in this manner, and suppose that p comes out true in the first yes-no experiment, but q alters conditions so that p later comes out false. Kpp would then, on the necessity interpretation, come out false in the world of the first pair of yes-no experiments, while p would be true there, making CpKpp false.
The concept of conjunction (and so also of disjunction, defined in terms of K and N) as somehow "modalized" is interesting. If conjunction is a kind of necessity and disjunction a kind of possibility, CKpAqrAKpqr, which introduces the distributive laws, becomes closely analogous to CLMpMLp (L for necessity, M for possibility) which fails in the systems contained in S5. But the modalization of K would also have to be of a sort which would leave provable CpKpp, whose modal analog would be CpLp. The modal interpretation of conjunction is, then, far from straightforward, but perhaps the suggestion of modality can provide us with some insight into the properties of other possible connectives of quantum logic. We intend to emphasize implication, and shall apply some of Jauch's insights to it. The implication Cpq is regarded as coming out false iff q is false while p is true. If we wish to apply the 'compound filter' concept to the truth of Cpq we shall say that Cpq comes out false in a world (filter) w iff in some world accessible to w (as determined by the sequence of the compound filter set up to test p and q) q comes out false while p is true. C in this case would acquire the properties of a necessary (or 'strict') implication. We note that the properties of the accessibility relation as determined by the sequence of experiments include at least transitivity and reflexivity--which are the properties of this relation in frames characteristic of the system S4. This suggests the possibility that one of the implications appropriate to quantum logic might have properties of the strict implication of S4. We shall then investigate the addition of S4 strict implication to the general orthomodular lattice (OML) .
Strict implications, OML's, and modularity: A number of approaches are available here. In Hacking's [5], S4 with strict implication primitive is discussed; note that the basic Hilbert-style axiomatization there employs an explicit statement of distributivity:
| DIST | CKpAqrAKpqKpr |
(C = strict implication).
Lattice-theoretically, the weakened distributivity that is orthomodularity may
be added to an orthocomplemented (OC) lattice (![]() as orthocomplement) by the OM law:
as orthocomplement) by the OM law:
| If x £ y,
then y £ (x |
This suggests replacing DIST in Hacking's formulation by
| OM | CCpqCqAKNpqp |
Another approach would be to add to a formulation sufficient for an OM L <W, £> a function É: W ´ W ® W, defined by
| É1: | p Ù (p É q) £ q | ||
| É2: | If r Ù p £ q, then r £ p É q, provided r is a meet of implications. |
The result of either of these equivalent approaches is to define S4 strict implication on the general OML. That S4 strict implication does not make the distributive laws provable here is easily established; in fact, we may achieve a more general result. First, replacing D2 by
| É2': | If r Ù p £ q, then r £ p É q, | provided every component of r which names an element of the lattice is in the scope of an implication |
gives a base for S5 strict implication: With the sign of necessity, L, defined as usual by Lp = 1 É p, we have, for S5's :É with r as in :É2':
| (3) | r = Lr |
Consider now the OML L10, the smallest non-modular OML
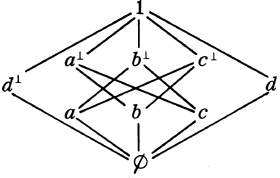
In L10, let p É q = 1 iff p £ q, = Æ otherwise. With É thus, É1 holds: if p £ q, then p É q = 1 and É1 is p £ q; if not-(p £ q), then pÉq = Æ and É1 is Æ £ q. So far as É2' is concerned, we have, by definition of L, Lr = 1 iff r = 1, = Æ otherwise. But as we have noted, for S5's É with r as in É2', Lr = r; if r = 1 and r Ù p £ q, then p £ q making p É q = 1 and so r £ p É q. If r ¹ 1, then by r = Lr we have r = Æ and so r £ p É q under any circumstances. But then :É1 and É2' obtain for L10 with É as indicated above. Since L10 is a non-modular OML, it then follows that the definition of S5 strict implication (or any strict implication included in S5) does not induce modularity and so a fortiori does not induce distributivity on an OML.
Strict implication and compatibility A central concept in OM theory is compatibility. We follow [10], p. 52 in saying that elements p and q are compatible in an orthocomplemented poset -- p C q -- provided:
| COMP |
There is an element e of the poset such that e
£ p, e £
q, and |
We are dealing with lattices, and so may convert the above to a condition
which is very expressive of the logical issues involved. Suppose p C
q; then the e whose existence is specified is such that e £
p Ù q, and in an OC
lattice, ( p Ù q)![]() £ e
£ e![]() .
Thus we may transform p Ù e
.
Thus we may transform p Ù e![]() £ q
£ q![]() to p Ù (p Ù
q)
to p Ù (p Ù
q)![]() £
q
£
q![]() . On the other hand, suppose
that p Ù (p Ù
q)
. On the other hand, suppose
that p Ù (p Ù
q)![]() £
q
£
q![]() .. Since p Ù
q £ p, £
q, p Ù q is itself the
e specified in COMP, and so we have p C
q iff p Ù (p Ù
q)
.. Since p Ù
q £ p, £
q, p Ù q is itself the
e specified in COMP, and so we have p C
q iff p Ù (p Ù
q)![]() £
q
£
q![]() . But in an OML, p C
q iff p p C q
. But in an OML, p C
q iff p p C q![]() ;
by the above we have p C q iff
p C q
;
by the above we have p C q iff
p C q![]() iff p Ù (p Ù
q
iff p Ù (p Ù
q![]() )
)![]() £
q; this latter is p Ù (p
£
q; this latter is p Ù (p![]() Ú q)
Ú q)![]() £
q. Our definition of compatibility then may be put:
£
q. Our definition of compatibility then may be put:
| COMP |
p C q iff p
Ù (p |
We may use this lattice-theoretical fact as the basis of definition for a binary logical function expressing compatibility:
Pab is defined as CKaANabb
Ppq is, of course, a classical thesis, but won't hold in general in quantum logic; it asserts, effectively, that classical modus ponens "works" for p and q and is a very appropriate logical definition of compatibility.
Let us conclude by establishing an interesting fact regarding compatibility and S4 modality: when S4 strict implication is defined on an OML; all such implications (and so all S4 modal functions) will be center-valued, i.e., universally compatible. First note that from
t Ù (t É r) £ r
and
s Ù (s É r) £ r
we may move, by the properties of meet and join, to
| (4) | (t É r) Ù (s É r) Ù (s Ú t) £ r |
Taking t = r (since r É r = 1) this becomes
| (5) | (s É r) Ù (s Ú r) £ r |
With s = (p É q)![]() this gives
this gives
| (6) | ((p É q) |
But in S4 we have
| (7) | p É q
£ ( p
É q) |
which with (6) gives
| (8) | ( p É q)
Ù ((p É
q) |
This is ( p É q) C r and,. since r may be any element, this gives the center-valuation of implications. QED
University of Florida
Gainesville, Florida