A Proof in
for (y)((x)Ax
É Ay)
Copyright, © 2004 by J. Jay Zeman
We shall display this proof in "ordinary" drawings of
Existential Graphs (executed in Adobe Illustrator and converted to GIF) on the
left and with an equivalent display executed in the EGControlLibrary application
(
) and saved from that application as SVG files. Since SVG is
not quite, as yet, a universal Web Graphics format, these are shown as converted
to GIF as well.
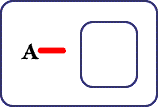
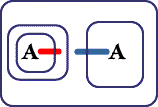
The first stage is, as usual, to set a Biclosure on the Sheet of Assertion as permitted by the rule of Positive Biclosure
 |
 |
| Figure 1. Biclosure inserted on SA | |
The next step involves insertion on Verso (i.e., in an Oddly Enclosed Area)
of a Spot with attached Line of Identity (Dot). At this point in
, the
facility to show connections between different LI's in a given Ligature is
turned off; the Graph inserted in
is a Spot with its attached LI "Stub"
and another segment of LI belonging to the same Ligature. There are a number of
ways to effect this in
, all of which would be legal according to the Beta
Rules.
 |
 |
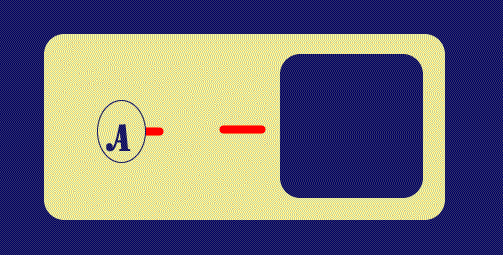| Figure 2. Insert a Graph on Verso | |
Next, the Spot is Reiterated into the "inner close," maintaining its connection to the original Ligature.
 |
 |
| Figure 3. Reiterate Beta Graph | |
Now another Biclosure is inserted, this time around the original Spot and its
LI Stub. In
this is best shown as taking two steps: the first is the
actual biclosure insertion, which here is shown to involve nothing resembling
the placement of a Graph in two distinct Areas - no Graph crosses a Cut. The
second phase of the operation here involves a Reiteration of the LI segment in
the outer Cut into the outer, Recto, area of the new Biclosure; this is
completely legal and brings into play the continuity of the Ligature across this
Biclosure as shown in the original "traditional" EG diagram on the left.
 |
 |
 |
|
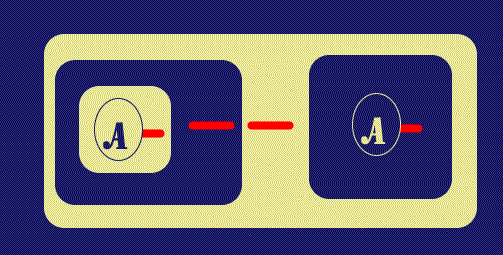| Figure 4. A Beta Biclosure | |
The next step is to break the Ligature (as represented in the
generated
diagram) by "Permission to break a LI on Recto (an Evenly-enclosed Line of
Identity);
is able to do this and to appropriately assign the components
of the original Ligature to either Ligature as appropriate; note the use of
color (in a manner similar to the way Peirce did it in manuscripts).
 |
 |
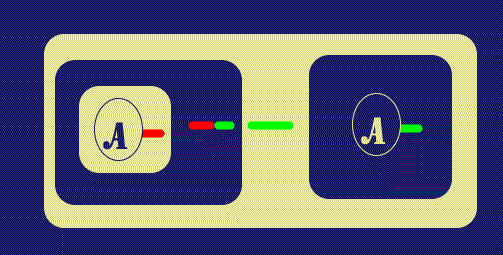| Figure 5. Break Line of Identity on Recto | |
Now, to complete the proof, withdraw the new Ligature from the outer close of
the second Biclosure; in
this is done by Deiterating the inner chunk of
Green LI back to the Green LI in the area enclosed by one Cut. The proof is
formally finished at this point, but it may be brought to a more Peircean iconic
state (emphasizing the continuity of identity) by making explicit visible
connections between certain Hooks within Ligatures, as in the second
diagram of this Figure.
 |
 |
 |
|
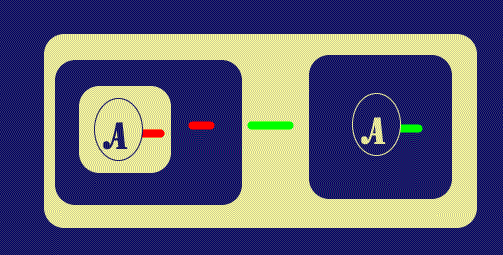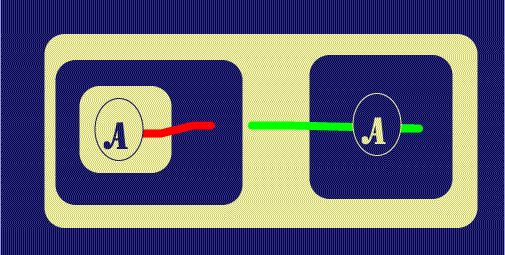| Figure 6. Withdraw Line of Identity end | |